| Non-Rationalised NCERT Books Solution | ||||||
|---|---|---|---|---|---|---|
| 6th | 7th | 8th | 9th | 10th | 11th | 12th |
| Content On This Page | ||
|---|---|---|
| Example 1 to 5 (Before Exercise 9.1) | Exercise 9.1 | Example 6 (Before Exercise 9.2) |
| Exercise 9.2 | ||
Chapter 9 Rational Numbers
Welcome to the solutions guide for Chapter 9: Rational Numbers. This chapter formally introduces a crucial expansion of our number system, moving beyond integers and simple fractions to encompass a broader set of numbers. Understanding rational numbers is fundamental for algebra and higher mathematics. A rational number is rigorously defined as any number that can be expressed in the form $\frac{p}{q}$, where $p$ and $q$ are both integers, and crucially, the denominator $q$ is not equal to zero ($q \neq 0$). This definition is the cornerstone of the chapter, and the solutions provided aim to solidify understanding of this concept and the operations involving these numbers.
The solutions clarify that the set of rational numbers includes all integers (since any integer $n$ can be written as $\frac{n}{1}$) and all familiar fractions (both positive and negative). Key foundational concepts explored include:
- Identifying Rational Numbers: Recognizing numbers that fit the $\frac{p}{q}$ definition.
- Equivalent Rational Numbers: Understanding that a rational number can be represented in infinitely many ways (e.g., $\frac{1}{2} = \frac{2}{4} = \frac{-3}{-6}$). Solutions demonstrate how to find equivalent forms by multiplying or dividing both the numerator ($p$) and the denominator ($q$) by the same non-zero integer.
- Standard Form: Reducing a rational number to its simplest or standard form. This requires two conditions: (1) the denominator ($q$) must be positive, and (2) the numerator ($p$) and the denominator ($q$) must have no common factors other than 1 (i.e., their Highest Common Factor, HCF, is 1). For example, $\frac{-12}{30}$ reduces to $\frac{-2}{5}$.
- Representation on the Number Line: Solutions illustrate how to accurately locate rational numbers on the number line by appropriately subdividing the intervals between integers based on the denominator.
A significant focus is placed on Comparing Rational Numbers. The solutions detail systematic methods:
- Using a Common Denominator: This is the primary method emphasized. It involves finding the Least Common Multiple (LCM) of the denominators of the rational numbers being compared, converting each rational number to an equivalent form with this LCM as the denominator, and then comparing the numerators.
- Converting to decimals might be mentioned but often takes a secondary role to the LCM method for formal comparison.
- Based on comparison, solutions guide students on arranging a given set of rational numbers in ascending or descending order.
The operational core of the chapter involves performing the four basic arithmetic operations:
- Addition and Subtraction: Solutions stress the necessity of finding a common denominator (usually the LCM) before adding or subtracting. Once the denominators are the same, the numerators are added or subtracted accordingly: $\frac{a}{d} + \frac{c}{d} = \frac{a+c}{d}$.
- Multiplication: This is more straightforward. Numerators are multiplied together, and denominators are multiplied together: $\frac{a}{b} \times \frac{c}{d} = \frac{a \times c}{b \times d}$. Simplification can often be done before or after multiplication.
- Division: Division by a rational number is defined as multiplication by its reciprocal (or multiplicative inverse). The reciprocal of $\frac{c}{d}$ (where $c \neq 0$) is $\frac{d}{c}$. Thus, the rule is: $\frac{a}{b} \div \frac{c}{d} = \frac{a}{b} \times \frac{d}{c}$ (provided $c \neq 0$).
The familiar properties of operations (Closure, Commutativity, Associativity), the roles of identity elements (Additive Identity 0, Multiplicative Identity 1), the existence of inverses (Additive Inverse $-\frac{p}{q}$, Multiplicative Inverse $\frac{q}{p}$ for non-zero rationals), and the Distributive Property of multiplication over addition/subtraction are revisited within the context of this expanded number system. Solutions may illustrate how these properties apply to rational numbers. Numerous numerical exercises and relevant word problems involving these operations are solved step-by-step, solidifying both conceptual understanding and computational fluency with rational numbers.
Example 1 to 5 (Before Exercise 9.1)
Example 1. Reduce $\frac{-45}{30}$ to the standard form.
Answer:
To reduce a rational number to its standard form, we need to divide its numerator and denominator by their greatest common divisor (GCD).
The given rational number is $\frac{-45}{30}$.
The numerator is -45 and the denominator is 30.
First, find the GCD of the absolute values of the numerator and the denominator, which are 45 and 30.
Factors of 45 are 1, 3, 5, 9, 15, 45.
Factors of 30 are 1, 2, 3, 5, 6, 10, 15, 30.
The common factors are 1, 3, 5, 15.
The greatest common divisor (GCD) of 45 and 30 is 15.
Now, divide both the numerator and the denominator of the given rational number by their GCD, 15.
$\frac{-45}{30} = \frac{-45 \div 15}{30 \div 15}$
$(-45) \div 15 = -3$
$30 \div 15 = 2$
So, $\frac{-45}{30} = \frac{-3}{2}$.
The standard form of a rational number has a positive denominator. In this case, the denominator is already positive (2). So, $\frac{-3}{2}$ is in the standard form.
Thus, the standard form of $\frac{-45}{30}$ is $\frac{-3}{2}$.
Example 2. Reduce to standard form:
(i) $\frac{36}{-24}$
(ii) $\frac{-3}{-15}$
Answer:
To reduce a rational number to its standard form, we need to divide its numerator and denominator by their greatest common divisor (GCD). Also, the standard form must have a positive denominator.
(i) Reduce $\frac{36}{-24}$ to standard form.
The numerator is 36 and the denominator is -24.
First, find the GCD of the absolute values of the numerator and the denominator, which are 36 and 24.
Factors of 36 are 1, 2, 3, 4, 6, 9, 12, 18, 36.
Factors of 24 are 1, 2, 3, 4, 6, 8, 12, 24.
The common factors are 1, 2, 3, 4, 6, 12.
The greatest common divisor (GCD) of 36 and 24 is 12.
Divide both the numerator and the denominator by 12:
$\frac{36}{-24} = \frac{36 \div 12}{-24 \div 12}$
$36 \div 12 = 3$
$(-24) \div 12 = -2$
So, $\frac{36}{-24} = \frac{3}{-2}$.
The standard form requires a positive denominator. We can rewrite $\frac{3}{-2}$ as $\frac{-3}{2}$ by multiplying both numerator and denominator by -1.
$\frac{3}{-2} = \frac{3 \times (-1)}{-2 \times (-1)} = \frac{-3}{2}$.
Thus, the standard form of $\frac{36}{-24}$ is $\frac{-3}{2}$.
(ii) Reduce $\frac{-3}{-15}$ to standard form.
The numerator is -3 and the denominator is -15.
First, make the denominator positive by multiplying the numerator and denominator by -1:
$\frac{-3}{-15} = \frac{-3 \times (-1)}{-15 \times (-1)} = \frac{3}{15}$.
Now, find the GCD of the absolute values of the numerator and the denominator of $\frac{3}{15}$, which are 3 and 15.
Factors of 3 are 1, 3.
Factors of 15 are 1, 3, 5, 15.
The greatest common divisor (GCD) of 3 and 15 is 3.
Divide both the numerator and the denominator by 3:
$\frac{3}{15} = \frac{3 \div 3}{15 \div 3}$
$3 \div 3 = 1$
$15 \div 3 = 5$
So, $\frac{3}{15} = \frac{1}{5}$.
The denominator is positive (5), and the numerator and denominator have no common factors other than 1. So, $\frac{1}{5}$ is in the standard form.
Thus, the standard form of $\frac{-3}{-15}$ is $\frac{1}{5}$.
Example 3. Do $\frac{4}{-9}$ and $\frac{-16}{36}$ represent the same rational number?
Answer:
To check if two rational numbers represent the same rational number, we can convert both of them to their standard form and compare them.
Consider the first rational number, $\frac{4}{-9}$.
The denominator is negative. To make it positive, we multiply the numerator and the denominator by $-1$.
$\frac{4}{-9} = \frac{4 \times (-1)}{-9 \times (-1)} = \frac{-4}{9}$
The standard form of $\frac{4}{-9}$ is $\frac{-4}{9}$.
Now consider the second rational number, $\frac{-16}{36}$.
To convert it to standard form, we find the greatest common divisor (GCD) of the absolute values of the numerator and the denominator.
Absolute value of numerator is $|-16| = 16$.
Absolute value of denominator is $|36| = 36$.
The factors of 16 are 1, 2, 4, 8, 16.
The factors of 36 are 1, 2, 3, 4, 6, 9, 12, 18, 36.
The GCD of 16 and 36 is 4.
Now, we divide the numerator and the denominator by their GCD, 4.
$\frac{-16}{36} = \frac{-16 \div 4}{36 \div 4} = \frac{-4}{9}$
The standard form of $\frac{-16}{36}$ is $\frac{-4}{9}$.
We found that the standard form of $\frac{4}{-9}$ is $\frac{-4}{9}$ and the standard form of $\frac{-16}{36}$ is $\frac{-4}{9}$.
Since their standard forms are equal, the two rational numbers represent the same rational number.
Yes, $\frac{4}{-9}$ and $\frac{-16}{36}$ represent the same rational number.
Example 4. List three rational numbers between – 2 and – 1.
Answer:
We want to find three rational numbers between $-2$ and $-1$.
First, we can write $-2$ and $-1$ as rational numbers with a common denominator.
Let's write them with denominator 1:
$-2 = \frac{-2}{1}$
$-1 = \frac{-1}{1}$
To find rational numbers between them, we can multiply the numerator and denominator of both fractions by a number greater than the number of rational numbers we need + 1. Since we need 3 rational numbers, we can multiply by $3+1=4$.
$-2 = \frac{-2 \times 4}{1 \times 4} = \frac{-8}{4}$
$-1 = \frac{-1 \times 4}{1 \times 4} = \frac{-4}{4}$
Now, we need to find three rational numbers between $\frac{-8}{4}$ and $\frac{-4}{4}$.
The integers between $-8$ and $-4$ are $-7$, $-6$, and $-5$.
So, the three rational numbers between $-2$ and $-1$ are $\frac{-7}{4}$, $\frac{-6}{4}$, and $\frac{-5}{4}$.
We can simplify $\frac{-6}{4}$ to $\frac{-3}{2}$.
Therefore, three rational numbers between $-2$ and $-1$ are $\frac{-7}{4}, \frac{-3}{2}, \frac{-5}{4}$.
Note: There are infinitely many rational numbers between any two distinct rational numbers. We could have multiplied by any integer greater than or equal to 4 to find three rational numbers. For example, multiplying by 5:
$-2 = \frac{-2 \times 5}{1 \times 5} = \frac{-10}{5}$
$-1 = \frac{-1 \times 5}{1 \times 5} = \frac{-5}{5}$
Three rational numbers between $\frac{-10}{5}$ and $\frac{-5}{5}$ are $\frac{-9}{5}, \frac{-8}{5}, \frac{-7}{5}$.
Example 5. Write four more numbers in the following pattern:
$$\frac{-1}{3} , \frac{-2}{6} , \frac{-3}{9} , \frac{-4}{12} ,...$$
Answer:
Given pattern:
$\frac{-1}{3} , \frac{-2}{6} , \frac{-3}{9} , \frac{-4}{12} ,...$
To Find:
Four more numbers in the given pattern.
Solution:
Let's observe the pattern in the given sequence of numbers.
The first term is $\frac{-1}{3}$.
The second term is $\frac{-2}{6}$. This can be written as $\frac{-1 \times 2}{3 \times 2}$.
The third term is $\frac{-3}{9}$. This can be written as $\frac{-1 \times 3}{3 \times 3}$.
The fourth term is $\frac{-4}{12}$. This can be written as $\frac{-1 \times 4}{3 \times 4}$.
From this observation, we can see that the $n^{th}$ term in the pattern is given by $\frac{-1 \times n}{3 \times n}$.
We need to find the next four terms, which correspond to $n=5, 6, 7, 8$.
For $n=5$, the term is $\frac{-1 \times 5}{3 \times 5} = \frac{-5}{15}$.
For $n=6$, the term is $\frac{-1 \times 6}{3 \times 6} = \frac{-6}{18}$.
For $n=7$, the term is $\frac{-1 \times 7}{3 \times 7} = \frac{-7}{21}$.
For $n=8$, the term is $\frac{-1 \times 8}{3 \times 8} = \frac{-8}{24}$.
Therefore, the next four numbers in the pattern are $\frac{-5}{15}, \frac{-6}{18}, \frac{-7}{21}, \frac{-8}{24}$.
The complete pattern including the next four terms is:
$\frac{-1}{3} , \frac{-2}{6} , \frac{-3}{9} , \frac{-4}{12} , \frac{-5}{15} , \frac{-6}{18} , \frac{-7}{21} , \frac{-8}{24} , ...$
Note that each of these fractions is equivalent to $\frac{-1}{3}$.
Exercise 9.1
Question 1. List five rational numbers between:
(i) –1 and 0
(ii) –2 and –1
(iii) $\frac{-4}{5}$ and $\frac{-2}{3}$
(iv) $-\frac{1}{2}$ and $\frac{2}{3}$
Answer:
(i) Rational numbers between –1 and 0
Given numbers: $-1$ and $0$.
To Find: Five rational numbers between $-1$ and $0$.
Solution:
We can write $-1$ and $0$ as rational numbers with a common denominator. Let's choose a denominator large enough to find five numbers between them. Since we need 5 numbers, we can multiply the numerator and denominator by $5 + 1 = 6$.
$-1 = \frac{-1}{1} = \frac{-1 \times 6}{1 \times 6} = \frac{-6}{6}$
$0 = \frac{0}{1} = \frac{0 \times 6}{1 \times 6} = \frac{0}{6}$
Now, we need to find five rational numbers between $\frac{-6}{6}$ and $\frac{0}{6}$.
The integers between $-6$ and $0$ are $-5, -4, -3, -2, -1$.
So, the five rational numbers are $\frac{-5}{6}, \frac{-4}{6}, \frac{-3}{6}, \frac{-2}{6}, \frac{-1}{6}$.
We can simplify some of these fractions:
$\frac{-4}{6} = \frac{-2}{3}$
$\frac{-3}{6} = \frac{-1}{2}$
$\frac{-2}{6} = \frac{-1}{3}$
Therefore, five rational numbers between $-1$ and $0$ are $\frac{-5}{6}, \frac{-2}{3}, \frac{-1}{2}, \frac{-1}{3}, \frac{-1}{6}$.
(ii) Rational numbers between –2 and –1
Given numbers: $-2$ and $-1$.
To Find: Five rational numbers between $-2$ and $-1$.
Solution:
We can write $-2$ and $-1$ as rational numbers with a common denominator. We need 5 numbers, so we multiply the numerator and denominator by $5 + 1 = 6$.
$-2 = \frac{-2}{1} = \frac{-2 \times 6}{1 \times 6} = \frac{-12}{6}$
$-1 = \frac{-1}{1} = \frac{-1 \times 6}{1 \times 6} = \frac{-6}{6}$
Now, we need to find five rational numbers between $\frac{-12}{6}$ and $\frac{-6}{6}$.
The integers between $-12$ and $-6$ are $-11, -10, -9, -8, -7$.
So, the five rational numbers are $\frac{-11}{6}, \frac{-10}{6}, \frac{-9}{6}, \frac{-8}{6}, \frac{-7}{6}$.
We can simplify some of these fractions:
$\frac{-10}{6} = \frac{-5}{3}$
$\frac{-9}{6} = \frac{-3}{2}$
$\frac{-8}{6} = \frac{-4}{3}$
Therefore, five rational numbers between $-2$ and $-1$ are $\frac{-11}{6}, \frac{-5}{3}, \frac{-3}{2}, \frac{-4}{3}, \frac{-7}{6}$.
(iii) Rational numbers between $\frac{-4}{5}$ and $\frac{-2}{3}$
Given numbers: $\frac{-4}{5}$ and $\frac{-2}{3}$.
To Find: Five rational numbers between $\frac{-4}{5}$ and $\frac{-2}{3}$.
Solution:
First, we need to make the denominators the same. The least common multiple (LCM) of the denominators 5 and 3 is 15.
$\frac{-4}{5} = \frac{-4 \times 3}{5 \times 3} = \frac{-12}{15}$
$\frac{-2}{3} = \frac{-2 \times 5}{3 \times 5} = \frac{-10}{15}$
We need five rational numbers between $\frac{-12}{15}$ and $\frac{-10}{15}$. There is only one integer ($-11$) between $-12$ and $-10$. So, we need to find equivalent fractions with a larger denominator.
Let's multiply the numerator and denominator of both equivalent fractions by 3 (we need 5 numbers, so we need at least $5+1=6$ spaces between the numerators. Currently, we have $ -10 - (-12) = 2$ spaces. Multiplying by $\frac{6}{2}=3$ should be sufficient).
$\frac{-12}{15} = \frac{-12 \times 3}{15 \times 3} = \frac{-36}{45}$
$\frac{-10}{15} = \frac{-10 \times 3}{15 \times 3} = \frac{-30}{45}$
Now, we need five rational numbers between $\frac{-36}{45}$ and $\frac{-30}{45}$.
The integers between $-36$ and $-30$ are $-35, -34, -33, -32, -31$.
So, the five rational numbers are $\frac{-35}{45}, \frac{-34}{45}, \frac{-33}{45}, \frac{-32}{45}, \frac{-31}{45}$.
We can simplify some of these fractions:
$\frac{-35}{45} = \frac{-7}{9}$
$\frac{-33}{45} = \frac{-11}{15}$
Therefore, five rational numbers between $\frac{-4}{5}$ and $\frac{-2}{3}$ are $\frac{-7}{9}, \frac{-34}{45}, \frac{-11}{15}, \frac{-32}{45}, \frac{-31}{45}$.
(iv) Rational numbers between $-\frac{1}{2}$ and $\frac{2}{3}$
Given numbers: $-\frac{1}{2}$ and $\frac{2}{3}$.
To Find: Five rational numbers between $-\frac{1}{2}$ and $\frac{2}{3}$.
Solution:
First, we make the denominators the same. The LCM of 2 and 3 is 6.
$-\frac{1}{2} = \frac{-1 \times 3}{2 \times 3} = \frac{-3}{6}$
$\frac{2}{3} = \frac{2 \times 2}{3 \times 2} = \frac{4}{6}$
Now, we need to find five rational numbers between $\frac{-3}{6}$ and $\frac{4}{6}$.
The integers between $-3$ and $4$ are $-2, -1, 0, 1, 2, 3$.
We can choose any five integers from this list. Let's choose $-2, -1, 0, 1, 2$.
So, five rational numbers are $\frac{-2}{6}, \frac{-1}{6}, \frac{0}{6}, \frac{1}{6}, \frac{2}{6}$.
We can simplify some of these fractions:
$\frac{-2}{6} = \frac{-1}{3}$
$\frac{0}{6} = 0$
$\frac{2}{6} = \frac{1}{3}$
Therefore, five rational numbers between $-\frac{1}{2}$ and $\frac{2}{3}$ are $\frac{-1}{3}, \frac{-1}{6}, 0, \frac{1}{6}, \frac{1}{3}$.
(Other possible answers exist, for example, choosing the integers $-1, 0, 1, 2, 3$ would give $\frac{-1}{6}, 0, \frac{1}{6}, \frac{1}{3}, \frac{1}{2}$).
Question 2. Write four more rational numbers in each of the following patterns:
(i) $\frac{-3}{5}$ , $\frac{-6}{10}$ , $\frac{-9}{15}$ , $\frac{-12}{20}$ ,......
(ii) $\frac{-1}{4}$ , $\frac{-2}{8}$ , $\frac{-3}{12}$ , ....…
(iii) $\frac{-1}{6}$ , $\frac{2}{-12}$ , $\frac{3}{-18}$ , $\frac{4}{-24}$ ,......
(iv) $\frac{-2}{3}$ , $\frac{2}{-3}$ , $\frac{4}{-6}$ , $\frac{6}{-9}$ ,..…
Answer:
(i) Pattern: $\frac{-3}{5}$ , $\frac{-6}{10}$ , $\frac{-9}{15}$ , $\frac{-12}{20}$ ,......
Observation:
The given numbers are equivalent fractions obtained by multiplying the numerator and denominator of $\frac{-3}{5}$ by consecutive integers 1, 2, 3, 4.
$\frac{-3}{5} = \frac{-3 \times 1}{5 \times 1}$
$\frac{-6}{10} = \frac{-3 \times 2}{5 \times 2}$
$\frac{-9}{15} = \frac{-3 \times 3}{5 \times 3}$
$\frac{-12}{20} = \frac{-3 \times 4}{5 \times 4}$
Next four terms:
We continue the pattern by multiplying by 5, 6, 7, and 8.
Next term ($n=5$): $\frac{-3 \times 5}{5 \times 5} = \frac{-15}{25}$
Next term ($n=6$): $\frac{-3 \times 6}{5 \times 6} = \frac{-18}{30}$
Next term ($n=7$): $\frac{-3 \times 7}{5 \times 7} = \frac{-21}{35}$
Next term ($n=8$): $\frac{-3 \times 8}{5 \times 8} = \frac{-24}{40}$
Therefore, the next four rational numbers in the pattern are $\frac{-15}{25}, \frac{-18}{30}, \frac{-21}{35}, \frac{-24}{40}$.
(ii) Pattern: $\frac{-1}{4}$ , $\frac{-2}{8}$ , $\frac{-3}{12}$ , ......
Observation:
The given numbers are equivalent fractions obtained by multiplying the numerator and denominator of $\frac{-1}{4}$ by consecutive integers 1, 2, 3.
$\frac{-1}{4} = \frac{-1 \times 1}{4 \times 1}$
$\frac{-2}{8} = \frac{-1 \times 2}{4 \times 2}$
$\frac{-3}{12} = \frac{-1 \times 3}{4 \times 3}$
Next four terms:
We continue the pattern by multiplying by 4, 5, 6, and 7.
Next term ($n=4$): $\frac{-1 \times 4}{4 \times 4} = \frac{-4}{16}$
Next term ($n=5$): $\frac{-1 \times 5}{4 \times 5} = \frac{-5}{20}$
Next term ($n=6$): $\frac{-1 \times 6}{4 \times 6} = \frac{-6}{24}$
Next term ($n=7$): $\frac{-1 \times 7}{4 \times 7} = \frac{-7}{28}$
Therefore, the next four rational numbers in the pattern are $\frac{-4}{16}, \frac{-5}{20}, \frac{-6}{24}, \frac{-7}{28}$.
(iii) Pattern: $\frac{-1}{6}$ , $\frac{2}{-12}$ , $\frac{3}{-18}$ , $\frac{4}{-24}$ ,......
Observation:
First, let's express all fractions with the negative sign in the numerator or denominator consistently. Note that $\frac{a}{-b} = \frac{-a}{b}$.
$\frac{2}{-12} = \frac{-2}{12}$
$\frac{3}{-18} = \frac{-3}{18}$
$\frac{4}{-24} = \frac{-4}{24}$
The pattern can be seen as equivalent fractions of $\frac{-1}{6}$, obtained by multiplying the numerator and denominator by consecutive integers 1, 2, 3, 4.
$\frac{-1}{6} = \frac{-1 \times 1}{6 \times 1}$
$\frac{2}{-12} = \frac{-2}{12} = \frac{-1 \times 2}{6 \times 2}$
$\frac{3}{-18} = \frac{-3}{18} = \frac{-1 \times 3}{6 \times 3}$
$\frac{4}{-24} = \frac{-4}{24} = \frac{-1 \times 4}{6 \times 4}$
To maintain the original pattern's format (positive numerator, negative denominator after the first term), the $n^{th}$ term (for $n \ge 2$) is $\frac{n}{-(6 \times n)}$.
Next four terms:
We continue the pattern for n = 5, 6, 7, 8.
Next term ($n=5$): $\frac{5}{-(6 \times 5)} = \frac{5}{-30}$
Next term ($n=6$): $\frac{6}{-(6 \times 6)} = \frac{6}{-36}$
Next term ($n=7$): $\frac{7}{-(6 \times 7)} = \frac{7}{-42}$
Next term ($n=8$): $\frac{8}{-(6 \times 8)} = \frac{8}{-48}$
Therefore, the next four rational numbers in the pattern are $\frac{5}{-30}, \frac{6}{-36}, \frac{7}{-42}, \frac{8}{-48}$.
(iv) Pattern: $\frac{-2}{3}$ , $\frac{2}{-3}$ , $\frac{4}{-6}$ , $\frac{6}{-9}$ ,......
Observation:
Note that $\frac{-2}{3} = \frac{2}{-3}$. All the terms in the sequence are equivalent to $\frac{-2}{3}$.
Let's examine the terms starting from the second term:
Term 2: $\frac{2}{-3} = \frac{2 \times 1}{-3 \times 1}$
Term 3: $\frac{4}{-6} = \frac{2 \times 2}{-3 \times 2}$
Term 4: $\frac{6}{-9} = \frac{2 \times 3}{-3 \times 3}$
The pattern seems to be generating fractions of the form $\frac{2 \times n}{-3 \times n}$ for $n=1, 2, 3, ...$ starting from the second term.
Next four terms:
We continue the pattern for n = 4, 5, 6, 7.
Next term ($n=4$): $\frac{2 \times 4}{-3 \times 4} = \frac{8}{-12}$
Next term ($n=5$): $\frac{2 \times 5}{-3 \times 5} = \frac{10}{-15}$
Next term ($n=6$): $\frac{2 \times 6}{-3 \times 6} = \frac{12}{-18}$
Next term ($n=7$): $\frac{2 \times 7}{-3 \times 7} = \frac{14}{-21}$
Therefore, the next four rational numbers in the pattern are $\frac{8}{-12}, \frac{10}{-15}, \frac{12}{-18}, \frac{14}{-21}$.
Question 3. Give four rational numbers equivalent to:
(i) $\frac{-2}{7}$
(ii) $\frac{5}{-3}$
(iii) $\frac{4}{9}$
Answer:
Concept:
Equivalent rational numbers can be obtained by multiplying (or dividing) both the numerator and the denominator of a given rational number by the same non-zero integer.
If $\frac{p}{q}$ is a rational number, then $\frac{p \times n}{q \times n}$ is an equivalent rational number for any non-zero integer $n$.
(i) Equivalent to $\frac{-2}{7}$
Given rational number: $\frac{-2}{7}$
To Find: Four equivalent rational numbers.
Solution:
We can multiply the numerator and denominator by different integers (e.g., 2, 3, 4, 5).
1. Multiplying by 2: $\frac{-2 \times 2}{7 \times 2} = \frac{-4}{14}$
2. Multiplying by 3: $\frac{-2 \times 3}{7 \times 3} = \frac{-6}{21}$
3. Multiplying by 4: $\frac{-2 \times 4}{7 \times 4} = \frac{-8}{28}$
4. Multiplying by 5: $\frac{-2 \times 5}{7 \times 5} = \frac{-10}{35}$
Therefore, four rational numbers equivalent to $\frac{-2}{7}$ are $\frac{-4}{14}, \frac{-6}{21}, \frac{-8}{28}, \frac{-10}{35}$.
(ii) Equivalent to $\frac{5}{-3}$
Given rational number: $\frac{5}{-3}$
To Find: Four equivalent rational numbers.
Solution:
We can multiply the numerator and denominator by different integers (e.g., 2, 3, 4, 5).
1. Multiplying by 2: $\frac{5 \times 2}{-3 \times 2} = \frac{10}{-6}$
2. Multiplying by 3: $\frac{5 \times 3}{-3 \times 3} = \frac{15}{-9}$
3. Multiplying by 4: $\frac{5 \times 4}{-3 \times 4} = \frac{20}{-12}$
4. Multiplying by 5: $\frac{5 \times 5}{-3 \times 5} = \frac{25}{-15}$
Note: $\frac{5}{-3}$ is equivalent to $\frac{-5}{3}$. We could also find equivalent fractions like $\frac{-10}{6}, \frac{-15}{9}$, etc.
Therefore, four rational numbers equivalent to $\frac{5}{-3}$ are $\frac{10}{-6}, \frac{15}{-9}, \frac{20}{-12}, \frac{25}{-15}$.
(iii) Equivalent to $\frac{4}{9}$
Given rational number: $\frac{4}{9}$
To Find: Four equivalent rational numbers.
Solution:
We can multiply the numerator and denominator by different integers (e.g., 2, 3, 4, 5).
1. Multiplying by 2: $\frac{4 \times 2}{9 \times 2} = \frac{8}{18}$
2. Multiplying by 3: $\frac{4 \times 3}{9 \times 3} = \frac{12}{27}$
3. Multiplying by 4: $\frac{4 \times 4}{9 \times 4} = \frac{16}{36}$
4. Multiplying by 5: $\frac{4 \times 5}{9 \times 5} = \frac{20}{45}$
Therefore, four rational numbers equivalent to $\frac{4}{9}$ are $\frac{8}{18}, \frac{12}{27}, \frac{16}{36}, \frac{20}{45}$.
Question 4. Draw the number line and represent the following rational numbers on it:
(i) $\frac{3}{4}$
(ii) $\frac{-5}{8}$
(iii) $\frac{-7}{4}$
(iv) $\frac{7}{8}$
Answer:
To represent a rational number on the number line, we follow these general steps:
1. Draw a number line and mark the point 0.
2. If the rational number is positive, we move to the right of 0. If it is negative, we move to the left of 0.
3. We divide the line segment between two consecutive integers into the number of equal parts given by the denominator of the rational number.
4. We then move the number of steps given by the numerator from the appropriate integer.
(i) $\frac{3}{4}$
This is a positive rational number that lies between 0 and 1.
Steps:
1. Draw a number line.
2. Divide the segment between the integers 0 and 1 into 4 equal parts (as the denominator is 4).
3. Starting from 0, move 3 parts to the right (as the numerator is 3).
4. The point reached is the representation of $\frac{3}{4}$ on the number line.
(ii) $\frac{-5}{8}$
This is a negative rational number that lies between 0 and -1.
Steps:
1. Draw a number line.
2. Divide the segment between the integers 0 and -1 into 8 equal parts (as the denominator is 8).
3. Starting from 0, move 5 parts to the left (as the numerator is 5 and the number is negative).
4. The point reached is the representation of $\frac{-5}{8}$ on the number line.
(iii) $\frac{-7}{4}$
This is an improper fraction. First, we convert it to a mixed fraction to understand its position.
$\frac{-7}{4} = -1\frac{3}{4}$
This shows that the number lies between -1 and -2.
Steps:
1. Draw a number line that includes the integers -2, -1, and 0.
2. Divide the segment between the integers -1 and -2 into 4 equal parts (as the denominator is 4).
3. Starting from -1, move 3 parts to the left (as the numerator of the fractional part is 3).
4. The point reached is the representation of $-1\frac{3}{4}$ or $\frac{-7}{4}$ on the number line.
(iv) $\frac{7}{8}$
This is a positive rational number that lies between 0 and 1.
Steps:
1. Draw a number line.
2. Divide the segment between the integers 0 and 1 into 8 equal parts (as the denominator is 8).
3. Starting from 0, move 7 parts to the right (as the numerator is 7).
4. The point reached is the representation of $\frac{7}{8}$ on the number line.
Question 5. The points P, Q, R, S, T, U, A and B on the number line are such that, TR = RS = SU and AP = PQ = QB. Name the rational numbers represented by P, Q, R and S.
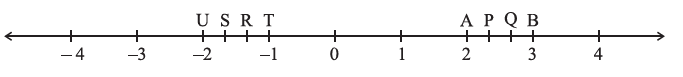
Answer:
To find the rational numbers represented by P, Q, R, and S, we need to analyze the divisions on the number line.
Finding the rational numbers for P and Q:
The points P and Q are located between the integers 2 and 3.
The condition AP = PQ = QB tells us that the segment between A (at 2) and B (at 3) is divided into 3 equal parts.
The total length of this segment is $3 - 2 = 1$.
Each of the three smaller parts (AP, PQ, QB) has a length of $\frac{1}{3}$.
To find the value of P, we start at A (which is 2) and add the length of one part (AP).
P = $2 + \frac{1}{3} = \frac{6}{3} + \frac{1}{3} = \frac{7}{3}$
To find the value of Q, we start at A (which is 2) and add the length of two parts (AP + PQ).
Q = $2 + \frac{1}{3} + \frac{1}{3} = 2 + \frac{2}{3} = \frac{6}{3} + \frac{2}{3} = \frac{8}{3}$
So, P represents $\frac{7}{3}$ and Q represents $\frac{8}{3}$.
Finding the rational numbers for R and S:
The points R and S are located between the integers -1 and -2.
The condition TR = RS = SU tells us that the segment between T (at -1) and U (at -2) is divided into 3 equal parts.
The total length of this segment is $|-2 - (-1)| = |-1| = 1$.
Each of the three smaller parts (TR, RS, SU) has a length of $\frac{1}{3}$.
To find the value of R, we start at T (which is -1) and move one part to the left (a distance of $\frac{1}{3}$).
R = $-1 - \frac{1}{3} = -\frac{3}{3} - \frac{1}{3} = -\frac{4}{3}$
To find the value of S, we start at T (which is -1) and move two parts to the left (a distance of $\frac{2}{3}$).
S = $-1 - \frac{1}{3} - \frac{1}{3} = -1 - \frac{2}{3} = -\frac{3}{3} - \frac{2}{3} = -\frac{5}{3}$
So, R represents $\frac{-4}{3}$ and S represents $\frac{-5}{3}$.
Summary:
P = $\frac{7}{3}$
Q = $\frac{8}{3}$
R = $\frac{-4}{3}$
S = $\frac{-5}{3}$
Question 6. Which of the following pairs represent the same rational number?
(i) $\frac{-7}{21}$ and $\frac{3}{9}$
(ii) $\frac{-16}{20}$ and $\frac{20}{-25}$
(iii) $\frac{-2}{-3}$ and $\frac{2}{3}$
(iv) $\frac{-3}{5}$ and $\frac{-12}{20}$
(v) $\frac{8}{-5}$ and $\frac{-24}{15}$
(vi) $\frac{1}{3}$ and $\frac{-1}{9}$
(vii) $\frac{-5}{-9}$ and $\frac{5}{-9}$
Answer:
To determine if a pair of rational numbers represents the same value, we can simplify each rational number to its standard form (lowest terms with a positive denominator) and compare them.
(i) $\frac{-7}{21}$ and $\frac{3}{9}$
Simplify $\frac{-7}{21}$: The greatest common divisor (GCD) of 7 and 21 is 7.
$\frac{-7}{21} = \frac{-7 \div 7}{21 \div 7} = \frac{-1}{3}$
Simplify $\frac{3}{9}$: The GCD of 3 and 9 is 3.
$\frac{3}{9} = \frac{3 \div 3}{9 \div 3} = \frac{1}{3}$
Comparing the standard forms, $\frac{-1}{3} \neq \frac{1}{3}$.
Therefore, this pair does not represent the same rational number.
(ii) $\frac{-16}{20}$ and $\frac{20}{-25}$
Simplify $\frac{-16}{20}$: The GCD of 16 and 20 is 4.
$\frac{-16}{20} = \frac{-16 \div 4}{20 \div 4} = \frac{-4}{5}$
Simplify $\frac{20}{-25}$: First write it in standard form with a positive denominator: $\frac{-20}{25}$. The GCD of 20 and 25 is 5.
$\frac{-20}{25} = \frac{-20 \div 5}{25 \div 5} = \frac{-4}{5}$
Comparing the standard forms, $\frac{-4}{5} = \frac{-4}{5}$.
Therefore, this pair does represent the same rational number.
(iii) $\frac{-2}{-3}$ and $\frac{2}{3}$
Simplify $\frac{-2}{-3}$: Since both numerator and denominator are negative, the fraction is positive.
$\frac{-2}{-3} = \frac{2}{3}$
The fraction $\frac{2}{3}$ is already in its standard form.
Comparing the standard forms, $\frac{2}{3} = \frac{2}{3}$.
Therefore, this pair does represent the same rational number.
(iv) $\frac{-3}{5}$ and $\frac{-12}{20}$
The fraction $\frac{-3}{5}$ is already in its standard form.
Simplify $\frac{-12}{20}$: The GCD of 12 and 20 is 4.
$\frac{-12}{20} = \frac{-12 \div 4}{20 \div 4} = \frac{-3}{5}$
Comparing the standard forms, $\frac{-3}{5} = \frac{-3}{5}$.
Therefore, this pair does represent the same rational number.
(v) $\frac{8}{-5}$ and $\frac{-24}{15}$
Simplify $\frac{8}{-5}$: Write it in standard form with a positive denominator: $\frac{-8}{5}$. This is already in lowest terms.
Simplify $\frac{-24}{15}$: The GCD of 24 and 15 is 3.
$\frac{-24}{15} = \frac{-24 \div 3}{15 \div 3} = \frac{-8}{5}$
Comparing the standard forms, $\frac{-8}{5} = \frac{-8}{5}$.
Therefore, this pair does represent the same rational number.
(vi) $\frac{1}{3}$ and $\frac{-1}{9}$
Both $\frac{1}{3}$ and $\frac{-1}{9}$ are already in their standard forms.
Comparing them, $\frac{1}{3} \neq \frac{-1}{9}$.
Therefore, this pair does not represent the same rational number.
(vii) $\frac{-5}{-9}$ and $\frac{5}{-9}$
Simplify $\frac{-5}{-9}$: Since both numerator and denominator are negative, the fraction is positive.
$\frac{-5}{-9} = \frac{5}{9}$. This is in standard form.
Simplify $\frac{5}{-9}$: Write it in standard form with a positive denominator: $\frac{-5}{9}$. This is in standard form.
Comparing the standard forms, $\frac{5}{9} \neq \frac{-5}{9}$.
Therefore, this pair does not represent the same rational number.
Conclusion: The pairs that represent the same rational number are (ii), (iii), (iv), and (v).
Question 7. Rewrite the following rational numbers in the simplest form:
(i) $\frac{-8}{6}$
(ii) $\frac{25}{45}$
(iii) $\frac{-44}{72}$
(iv) $\frac{-8}{10}$
Answer:
Concept:
A rational number $\frac{p}{q}$ is said to be in its simplest form (or standard form or lowest terms) if $p$ and $q$ have no common factors other than 1 (i.e., they are co-prime) and the denominator $q$ is positive.
To convert a rational number to its simplest form, we divide both the numerator and the denominator by their greatest common divisor (GCD or HCF).
(i) $\frac{-8}{6}$
Given rational number: $\frac{-8}{6}$
Solution:
The numerator is -8 and the denominator is 6.
We find the greatest common divisor (GCD) of the absolute values of the numerator and denominator, i.e., GCD(8, 6).
Factors of 8 are 1, 2, 4, 8.
Factors of 6 are 1, 2, 3, 6.
The GCD(8, 6) is 2.
Now, we divide both the numerator and the denominator by their GCD, which is 2:
$\frac{-8 \div 2}{6 \div 2} = \frac{-4}{3}$
The denominator (3) is positive, and the GCD of 4 and 3 is 1. So, this is the simplest form.
Therefore, the simplest form of $\frac{-8}{6}$ is $\frac{-4}{3}$.
(ii) $\frac{25}{45}$
Given rational number: $\frac{25}{45}$
Solution:
The numerator is 25 and the denominator is 45.
We find the GCD(25, 45).
Factors of 25 are 1, 5, 25.
Factors of 45 are 1, 3, 5, 9, 15, 45.
The GCD(25, 45) is 5.
Now, we divide both the numerator and the denominator by their GCD, which is 5:
$\frac{25 \div 5}{45 \div 5} = \frac{5}{9}$
The denominator (9) is positive, and the GCD of 5 and 9 is 1. So, this is the simplest form.
Therefore, the simplest form of $\frac{25}{45}$ is $\frac{5}{9}$.
(iii) $\frac{-44}{72}$
Given rational number: $\frac{-44}{72}$
Solution:
The numerator is -44 and the denominator is 72.
We find the GCD(44, 72).
Factors of 44 are 1, 2, 4, 11, 22, 44.
Factors of 72 are 1, 2, 3, 4, 6, 8, 9, 12, 18, 24, 36, 72.
The GCD(44, 72) is 4.
Now, we divide both the numerator and the denominator by their GCD, which is 4:
$\frac{-44 \div 4}{72 \div 4} = \frac{-11}{18}$
The denominator (18) is positive, and the GCD of 11 and 18 is 1. So, this is the simplest form.
Therefore, the simplest form of $\frac{-44}{72}$ is $\frac{-11}{18}$.
(iv) $\frac{-8}{10}$
Given rational number: $\frac{-8}{10}$
Solution:
The numerator is -8 and the denominator is 10.
We find the GCD(8, 10).
Factors of 8 are 1, 2, 4, 8.
Factors of 10 are 1, 2, 5, 10.
The GCD(8, 10) is 2.
Now, we divide both the numerator and the denominator by their GCD, which is 2:
$\frac{-8 \div 2}{10 \div 2} = \frac{-4}{5}$
The denominator (5) is positive, and the GCD of 4 and 5 is 1. So, this is the simplest form.
Therefore, the simplest form of $\frac{-8}{10}$ is $\frac{-4}{5}$.
Question 8. Fill in the boxes with the correct symbol out of >, <, and =.
(i) $\frac{-5}{7}$ ⬜ $\frac{2}{3}$
(ii) $\frac{-4}{5}$ ⬜ $\frac{-5}{7}$
(iii) $\frac{-7}{8}$ ⬜ $\frac{14}{-16}$
(iv) $\frac{-8}{5}$ ⬜ $\frac{-7}{4}$
(v) $\frac{1}{-3}$ ⬜ $\frac{-1}{4}$
(vi) $\frac{5}{-11}$ ⬜ $\frac{-5}{11}$
(vii) 0 ⬜ $\frac{-7}{6}$
Answer:
To compare two rational numbers, we can make their denominators positive and then find a common denominator (like the LCM) or use cross-multiplication.
(i) $\frac{-5}{7}$ ☐ $\frac{2}{3}$
$\frac{-5}{7}$ is a negative rational number.
$\frac{2}{3}$ is a positive rational number.
Any negative rational number is always less than any positive rational number.
Therefore, $\frac{-5}{7} < \frac{2}{3}$.
The correct symbol is <.
$\frac{-5}{7}$ < $\frac{2}{3}$
(ii) $\frac{-4}{5}$ ☐ $\frac{-5}{7}$
Both numbers are negative. The denominators are positive.
We find a common denominator, which is the LCM of 5 and 7. LCM(5, 7) = 35.
$\frac{-4}{5} = \frac{-4 \times 7}{5 \times 7} = \frac{-28}{35}$
$\frac{-5}{7} = \frac{-5 \times 5}{7 \times 5} = \frac{-25}{35}$
Now, we compare the numerators -28 and -25.
Since $-28 < -25$, we have $\frac{-28}{35} < \frac{-25}{35}$.
Therefore, $\frac{-4}{5} < \frac{-5}{7}$.
The correct symbol is <.
$\frac{-4}{5}$ < $\frac{-5}{7}$
(iii) $\frac{-7}{8}$ ☐ $\frac{14}{-16}$
First, write $\frac{14}{-16}$ with a positive denominator: $\frac{-14}{16}$.
Now compare $\frac{-7}{8}$ and $\frac{-14}{16}$.
We can simplify $\frac{-14}{16}$ by dividing the numerator and denominator by their GCD, which is 2.
$\frac{-14 \div 2}{16 \div 2} = \frac{-7}{8}$
Both rational numbers are equal to $\frac{-7}{8}$.
Therefore, $\frac{-7}{8} = \frac{14}{-16}$.
The correct symbol is =.
$\frac{-7}{8}$ = $\frac{14}{-16}$
(iv) $\frac{-8}{5}$ ☐ $\frac{-7}{4}$
Both numbers are negative. The denominators are positive.
We find a common denominator, which is the LCM of 5 and 4. LCM(5, 4) = 20.
$\frac{-8}{5} = \frac{-8 \times 4}{5 \times 4} = \frac{-32}{20}$
$\frac{-7}{4} = \frac{-7 \times 5}{4 \times 5} = \frac{-35}{20}$
Now, we compare the numerators -32 and -35.
Since $-32 > -35$, we have $\frac{-32}{20} > \frac{-35}{20}$.
Therefore, $\frac{-8}{5} > \frac{-7}{4}$.
The correct symbol is >.
$\frac{-8}{5}$ > $\frac{-7}{4}$
(v) $\frac{1}{-3}$ ☐ $\frac{-1}{4}$
First, write $\frac{1}{-3}$ with a positive denominator: $\frac{-1}{3}$.
Now compare $\frac{-1}{3}$ and $\frac{-1}{4}$.
Both numbers are negative. The denominators are positive.
We find a common denominator, which is the LCM of 3 and 4. LCM(3, 4) = 12.
$\frac{-1}{3} = \frac{-1 \times 4}{3 \times 4} = \frac{-4}{12}$
$\frac{-1}{4} = \frac{-1 \times 3}{4 \times 3} = \frac{-3}{12}$
Now, we compare the numerators -4 and -3.
Since $-4 < -3$, we have $\frac{-4}{12} < \frac{-3}{12}$.
Therefore, $\frac{-1}{3} < \frac{-1}{4}$, which means $\frac{1}{-3} < \frac{-1}{4}$.
The correct symbol is <.
$\frac{1}{-3}$ < $\frac{-1}{4}$
(vi) $\frac{5}{-11}$ ☐ $\frac{-5}{11}$
First, write $\frac{5}{-11}$ with a positive denominator: $\frac{-5}{11}$.
Now compare $\frac{-5}{11}$ and $\frac{-5}{11}$.
The two rational numbers are identical.
Therefore, $\frac{5}{-11} = \frac{-5}{11}$.
The correct symbol is =.
$\frac{5}{-11}$ = $\frac{-5}{11}$
(vii) 0 ☐ $\frac{-7}{6}$
We are comparing 0 with a negative rational number $\frac{-7}{6}$.
Zero is always greater than any negative number.
Therefore, $0 > \frac{-7}{6}$.
The correct symbol is >.
0 > $\frac{-7}{6}$
Question 9. Which is greater in each of the following:
(i) $\frac{2}{3}$ , $\frac{5}{2}$
(ii) $\frac{-5}{6}$ , $\frac{-4}{3}$
(iii) $\frac{-3}{4}$ , $\frac{2}{-3}$
(iv) $\frac{-1}{4}$ , $\frac{1}{4}$
(v) $-3\frac{2}{7}$ , $-3\frac{4}{5}$
Answer:
To find the greater rational number in each pair, we can convert them to equivalent rational numbers with a common positive denominator and compare their numerators.
(i) $\frac{2}{3}$ , $\frac{5}{2}$
Both rational numbers are positive.
The denominators are 3 and 2. The Least Common Multiple (LCM) of 3 and 2 is 6.
Convert the fractions to have a denominator of 6:
$\frac{2}{3} = \frac{2 \times 2}{3 \times 2} = \frac{4}{6}$
$\frac{5}{2} = \frac{5 \times 3}{2 \times 3} = \frac{15}{6}$
Compare the numerators 4 and 15. Since $15 > 4$, we have $\frac{15}{6} > \frac{4}{6}$.
Therefore, $\frac{5}{2}$ is greater than $\frac{2}{3}$.
(ii) $\frac{-5}{6}$ , $\frac{-4}{3}$
Both rational numbers are negative.
The denominators are 6 and 3. The LCM of 6 and 3 is 6.
Convert $\frac{-4}{3}$ to have a denominator of 6:
$\frac{-4}{3} = \frac{-4 \times 2}{3 \times 2} = \frac{-8}{6}$
Now compare $\frac{-5}{6}$ and $\frac{-8}{6}$. Compare the numerators -5 and -8.
Since $-5 > -8$, we have $\frac{-5}{6} > \frac{-8}{6}$.
Therefore, $\frac{-5}{6}$ is greater than $\frac{-4}{3}$.
(iii) $\frac{-3}{4}$ , $\frac{2}{-3}$
First, write $\frac{2}{-3}$ in standard form with a positive denominator: $\frac{-2}{3}$.
Now compare $\frac{-3}{4}$ and $\frac{-2}{3}$. Both are negative.
The denominators are 4 and 3. The LCM of 4 and 3 is 12.
Convert the fractions to have a denominator of 12:
$\frac{-3}{4} = \frac{-3 \times 3}{4 \times 3} = \frac{-9}{12}$
$\frac{-2}{3} = \frac{-2 \times 4}{3 \times 4} = \frac{-8}{12}$
Compare the numerators -9 and -8. Since $-8 > -9$, we have $\frac{-8}{12} > \frac{-9}{12}$.
Therefore, $\frac{-2}{3} > \frac{-3}{4}$. This means $\frac{2}{-3}$ is greater than $\frac{-3}{4}$.
(iv) $\frac{-1}{4}$ , $\frac{1}{4}$
$\frac{-1}{4}$ is a negative rational number.
$\frac{1}{4}$ is a positive rational number.
Any positive rational number is always greater than any negative rational number.
Therefore, $\frac{1}{4}$ is greater than $\frac{-1}{4}$.
(v) $-3\frac{2}{7}$ , $-3\frac{4}{5}$
First, convert the mixed fractions into improper fractions.
$-3\frac{2}{7} = -\frac{(3 \times 7) + 2}{7} = -\frac{21 + 2}{7} = \frac{-23}{7}$
$-3\frac{4}{5} = -\frac{(3 \times 5) + 4}{5} = -\frac{15 + 4}{5} = \frac{-19}{5}$
Now compare $\frac{-23}{7}$ and $\frac{-19}{5}$. Both are negative.
The denominators are 7 and 5. The LCM of 7 and 5 is 35.
Convert the fractions to have a denominator of 35:
$\frac{-23}{7} = \frac{-23 \times 5}{7 \times 5} = \frac{-115}{35}$
$\frac{-19}{5} = \frac{-19 \times 7}{5 \times 7} = \frac{-133}{35}$
Compare the numerators -115 and -133. Since $-115 > -133$, we have $\frac{-115}{35} > \frac{-133}{35}$.
Therefore, $\frac{-23}{7} > \frac{-19}{5}$. This means $-3\frac{2}{7}$ is greater than $-3\frac{4}{5}$.
Question 10. Write the following rational numbers in ascending order:
(i) $\frac{-3}{5}$ , $\frac{-2}{5}$ , $\frac{-1}{5}$
(ii) $\frac{-1}{3}$ , $\frac{-2}{9}$ , $\frac{-4}{3}$
(iii) $\frac{-3}{7}$ , $\frac{-3}{2}$ , $\frac{-3}{4}$
Answer:
(i) $\frac{-3}{5}$ , $\frac{-2}{5}$ , $\frac{-1}{5}$
Given rational numbers: $\frac{-3}{5}$, $\frac{-2}{5}$, $\frac{-1}{5}$.
To Order: Arrange the numbers in ascending order.
Solution:
The denominators of the given rational numbers are the same (5).
To arrange them in ascending order, we compare their numerators: -3, -2, -1.
We know that $-3 < -2 < -1$.
Since the denominators are positive and equal, the order of the rational numbers will be the same as the order of their numerators.
Therefore, $\frac{-3}{5} < \frac{-2}{5} < \frac{-1}{5}$.
The ascending order is: $\frac{-3}{5} , \frac{-2}{5} , \frac{-1}{5}$.
(ii) $\frac{-1}{3}$ , $\frac{-2}{9}$ , $\frac{-4}{3}$
Given rational numbers: $\frac{-1}{3}$, $\frac{-2}{9}$, $\frac{-4}{3}$.
To Order: Arrange the numbers in ascending order.
Solution:
First, we make the denominators of the rational numbers equal and positive.
The denominators are 3, 9, and 3. The Least Common Multiple (LCM) of 3 and 9 is 9.
Convert each rational number to an equivalent rational number with denominator 9:
$\frac{-1}{3} = \frac{-1 \times 3}{3 \times 3} = \frac{-3}{9}$
$\frac{-2}{9}$ (already has denominator 9)
$\frac{-4}{3} = \frac{-4 \times 3}{3 \times 3} = \frac{-12}{9}$
Now we have the numbers: $\frac{-3}{9}$, $\frac{-2}{9}$, $\frac{-12}{9}$.
Compare their numerators: -3, -2, -12.
Arranging the numerators in ascending order: $-12 < -3 < -2$.
So, the order of the rational numbers is: $\frac{-12}{9} < \frac{-3}{9} < \frac{-2}{9}$.
Replacing the equivalent fractions with the original numbers:
$\frac{-4}{3} < \frac{-1}{3} < \frac{-2}{9}$.
The ascending order is: $\frac{-4}{3} , \frac{-1}{3} , \frac{-2}{9}$.
(iii) $\frac{-3}{7}$ , $\frac{-3}{2}$ , $\frac{-3}{4}$
Given rational numbers: $\frac{-3}{7}$, $\frac{-3}{2}$, $\frac{-3}{4}$.
To Order: Arrange the numbers in ascending order.
Solution:
The numerators of the given rational numbers are the same (-3).
Method 1: Comparing positive counterparts
Consider the positive counterparts: $\frac{3}{7}$, $\frac{3}{2}$, $\frac{3}{4}$.
When comparing positive fractions with the same numerator, the fraction with the larger denominator is smaller.
Comparing denominators: 7, 2, 4. Order: $2 < 4 < 7$.
Therefore, the order of the positive fractions is $\frac{3}{7} < \frac{3}{4} < \frac{3}{2}$.
Since we are dealing with negative numbers, the inequality reverses.
So, $\frac{-3}{7} > \frac{-3}{4} > \frac{-3}{2}$.
Writing in ascending order: $\frac{-3}{2} < \frac{-3}{4} < \frac{-3}{7}$.
Method 2: Using common denominator
The denominators are 7, 2, 4. The LCM of 7, 2, and 4 is 28.
Convert each rational number to an equivalent rational number with denominator 28:
$\frac{-3}{7} = \frac{-3 \times 4}{7 \times 4} = \frac{-12}{28}$
$\frac{-3}{2} = \frac{-3 \times 14}{2 \times 14} = \frac{-42}{28}$
$\frac{-3}{4} = \frac{-3 \times 7}{4 \times 7} = \frac{-21}{28}$
Now we have the numbers: $\frac{-12}{28}$, $\frac{-42}{28}$, $\frac{-21}{28}$.
Compare their numerators: -12, -42, -21.
Arranging the numerators in ascending order: $-42 < -21 < -12$.
So, the order of the rational numbers is: $\frac{-42}{28} < \frac{-21}{28} < \frac{-12}{28}$.
Replacing the equivalent fractions with the original numbers:
$\frac{-3}{2} < \frac{-3}{4} < \frac{-3}{7}$.
The ascending order is: $\frac{-3}{2} , \frac{-3}{4} , \frac{-3}{7}$.
Example 6 (Before Exercise 9.2)
Example 6. Satpal walks $\frac{2}{3}$ km from a place P, towards east and then from there $1\frac{5}{7}$ km towards west. Where will he be now from P?
Answer:
Given:
Starting point is P.
Distance walked towards east from P = $\frac{2}{3}$ km.
Distance walked towards west from the new position = $1\frac{5}{7}$ km.
To Find:
Satpal's final position relative to the starting point P.
Solution:
Let's represent the eastward direction from P as positive (+) and the westward direction as negative (-).
The distance walked towards the east from P is $+\frac{2}{3}$ km.
The distance walked towards the west is $1\frac{5}{7}$ km.
First, convert the mixed fraction $1\frac{5}{7}$ into an improper fraction:
$1\frac{5}{7} = \frac{(1 \times 7) + 5}{7} = \frac{7 + 5}{7} = \frac{12}{7}$
Since this walk is towards the west, we represent this distance as $-\frac{12}{7}$ km relative to the direction convention.
Satpal's final position from P is the sum of the distances walked in each direction.
Final Position = (Distance walked east) + (Distance walked west)
Final Position = $\frac{2}{3} + (-\frac{12}{7})$
Final Position = $\frac{2}{3} - \frac{12}{7}$
To subtract these fractions, we need a common denominator. The Least Common Multiple (LCM) of 3 and 7 is 21.
Convert the fractions to equivalent fractions with a denominator of 21:
$\frac{2}{3} = \frac{2 \times 7}{3 \times 7} = \frac{14}{21}$
$\frac{12}{7} = \frac{12 \times 3}{7 \times 3} = \frac{36}{21}$
Now, substitute these back into the calculation:
Final Position = $\frac{14}{21} - \frac{36}{21} = \frac{14 - 36}{21} = \frac{-22}{21}$
The result is $\frac{-22}{21}$ km.
The negative sign indicates that the final position is to the west of the starting point P.
We can write the distance as a mixed fraction:
$\frac{-22}{21} = -1\frac{1}{21}$ km.
Therefore, Satpal will be $1\frac{1}{21}$ km towards the west from his starting point P.
Exercise 9.2
Question 1. Find the sum:
(i) $\frac{5}{4} + \left( \frac{-11}{4} \right)$
(ii) $\frac{5}{3} + \frac{3}{5}$
(iii) $\frac{-9}{10} + \frac{22}{15}$
(iv) $\frac{-3}{-11} + \frac{5}{9}$
(v) $\frac{-8}{19} + \frac{(-2)}{57}$
(vi) $\frac{-2}{3} + 0$
(vii) $-2\frac{1}{3} + 4\frac{3}{5}$
Answer:
(i) $\frac{5}{4} \ + \ \left( \frac{-11}{4} \right)$
Given expression: $\frac{5}{4} \ + \ \left( \frac{-11}{4} \right)$
Solution:
The denominators are the same (4).
So, we add the numerators:
$\frac{5 \ + \ (-11)}{4} \ = \ \frac{5 \ - \ 11}{4} \ = \ \frac{-6}{4}$
Simplify the fraction by dividing the numerator and denominator by their GCD, which is 2:
$\frac{-6 \div 2}{4 \div 2} \ = \ \frac{-3}{2}$
Therefore, the sum is $\frac{-3}{2}$.
(ii) $\frac{5}{3} \ + \ \frac{3}{5}$
Given expression: $\frac{5}{3} \ + \ \frac{3}{5}$
Solution:
The denominators are different (3 and 5).
Find the Least Common Multiple (LCM) of the denominators: LCM(3, 5) = 15.
Convert the fractions to equivalent fractions with denominator 15:
$\frac{5}{3} \ = \ \frac{5 \times 5}{3 \times 5} \ = \ \frac{25}{15}$
$\frac{3}{5} \ = \ \frac{3 \times 3}{5 \times 3} \ = \ \frac{9}{15}$
Now add the equivalent fractions:
$\frac{25}{15} \ + \ \frac{9}{15} \ = \ \frac{25 \ + \ 9}{15} \ = \ \frac{34}{15}$
Therefore, the sum is $\frac{34}{15}$.
(iii) $\frac{-9}{10} \ + \ \frac{22}{15}$
Given expression: $\frac{-9}{10} \ + \ \frac{22}{15}$
Solution:
The denominators are different (10 and 15).
Find the LCM of the denominators: LCM(10, 15) = 30.
Convert the fractions to equivalent fractions with denominator 30:
$\frac{-9}{10} \ = \ \frac{-9 \times 3}{10 \times 3} \ = \ \frac{-27}{30}$
$\frac{22}{15} \ = \ \frac{22 \times 2}{15 \times 2} \ = \ \frac{44}{30}$
Now add the equivalent fractions:
$\frac{-27}{30} \ + \ \frac{44}{30} \ = \ \frac{-27 \ + \ 44}{30} \ = \ \frac{17}{30}$
Therefore, the sum is $\frac{17}{30}$.
(iv) $\frac{-3}{-11} \ + \ \frac{5}{9}$
Given expression: $\frac{-3}{-11} \ + \ \frac{5}{9}$
Solution:
First, simplify $\frac{-3}{-11}$. Since both numerator and denominator are negative, the fraction is positive:
$\frac{-3}{-11} \ = \ \frac{3}{11}$
Now the expression is $\frac{3}{11} \ + \ \frac{5}{9}$.
The denominators are different (11 and 9).
Find the LCM of the denominators: LCM(11, 9) = 99.
Convert the fractions to equivalent fractions with denominator 99:
$\frac{3}{11} \ = \ \frac{3 \times 9}{11 \times 9} \ = \ \frac{27}{99}$
$\frac{5}{9} \ = \ \frac{5 \times 11}{9 \times 11} \ = \ \frac{55}{99}$
Now add the equivalent fractions:
$\frac{27}{99} \ + \ \frac{55}{99} \ = \ \frac{27 \ + \ 55}{99} \ = \ \frac{82}{99}$
Therefore, the sum is $\frac{82}{99}$.
(v) $\frac{-8}{19} \ + \ \frac{(-2)}{57}$
Given expression: $\frac{-8}{19} \ + \ \frac{-2}{57}$
Solution:
The denominators are different (19 and 57).
Find the LCM of the denominators: LCM(19, 57) = 57 (since $19 \times 3 \ = \ 57$).
Convert $\frac{-8}{19}$ to an equivalent fraction with denominator 57:
$\frac{-8}{19} \ = \ \frac{-8 \times 3}{19 \times 3} \ = \ \frac{-24}{57}$
Now add the fractions:
$\frac{-24}{57} \ + \ \frac{-2}{57} \ = \ \frac{-24 \ + \ (-2)}{57} \ = \ \frac{-24 \ - \ 2}{57} \ = \ \frac{-26}{57}$
Therefore, the sum is $\frac{-26}{57}$.
(vi) $\frac{-2}{3} \ + \ 0$
Given expression: $\frac{-2}{3} \ + \ 0$
Solution:
Adding 0 to any rational number results in the rational number itself (Additive Identity Property).
$\frac{-2}{3} \ + \ 0 \ = \ \frac{-2}{3}$
Therefore, the sum is $\frac{-2}{3}$.
(vii) $-2\frac{1}{3} \ + \ 4\frac{3}{5}$
Given expression: $-2\frac{1}{3} \ + \ 4\frac{3}{5}$
Solution:
First, convert the mixed fractions into improper fractions:
$-2\frac{1}{3} \ = \ -\frac{(2 \times 3) \ + \ 1}{3} \ = \ -\frac{6 \ + \ 1}{3} \ = \ \frac{-7}{3}$
$4\frac{3}{5} \ = \ \frac{(4 \times 5) \ + \ 3}{5} \ = \ \frac{20 \ + \ 3}{5} \ = \ \frac{23}{5}$
Now the expression is $\frac{-7}{3} \ + \ \frac{23}{5}$.
The denominators are different (3 and 5).
Find the LCM of the denominators: LCM(3, 5) = 15.
Convert the fractions to equivalent fractions with denominator 15:
$\frac{-7}{3} \ = \ \frac{-7 \times 5}{3 \times 5} \ = \ \frac{-35}{15}$
$\frac{23}{5} \ = \ \frac{23 \times 3}{5 \times 3} \ = \ \frac{69}{15}$
Now add the equivalent fractions:
$\frac{-35}{15} \ + \ \frac{69}{15} \ = \ \frac{-35 \ + \ 69}{15} \ = \ \frac{34}{15}$
We can convert this back to a mixed fraction:
$\frac{34}{15} \ = \ 2\frac{4}{15}$
Therefore, the sum is $\frac{34}{15}$ or $2\frac{4}{15}$.
Question 2. Find;
(i) $\frac{7}{24} - \frac{17}{36}$
(ii) $\frac{5}{63} - \left( \frac{-6}{21} \right)$
(iii) $\frac{-6}{13} - \left( \frac{-7}{15} \right)$
(iv) $\frac{-3}{8} - \frac{7}{11}$
(v) $-2\frac{1}{9} - 6$
Answer:
(i) $\frac{7}{24} \ - \ \frac{17}{36}$
Given expression: $\frac{7}{24} \ - \ \frac{17}{36}$
Solution:
The denominators are different (24 and 36).
Find the Least Common Multiple (LCM) of the denominators.
Prime factorization of 24: $2 \times 2 \times 2 \times 3 \ = \ 2^3 \times 3$
Prime factorization of 36: $2 \times 2 \times 3 \times 3 \ = \ 2^2 \times 3^2$
LCM(24, 36) = $2^3 \times 3^2 \ = \ 8 \times 9 \ = \ 72$.
Convert the fractions to equivalent fractions with denominator 72:
$\frac{7}{24} \ = \ \frac{7 \times 3}{24 \times 3} \ = \ \frac{21}{72}$
$\frac{17}{36} \ = \ \frac{17 \times 2}{36 \times 2} \ = \ \frac{34}{72}$
Now subtract the equivalent fractions:
$\frac{21}{72} \ - \ \frac{34}{72} \ = \ \frac{21 \ - \ 34}{72} \ = \ \frac{-13}{72}$
Therefore, the result is $\frac{-13}{72}$.
(ii) $\frac{5}{63} \ - \ \left( \frac{-6}{21} \right)$
Given expression: $\frac{5}{63} \ - \ \left( \frac{-6}{21} \right)$
Solution:
Subtracting a negative number is the same as adding the positive counterpart:
$\frac{5}{63} \ - \ \left( \frac{-6}{21} \right) \ = \ \frac{5}{63} \ + \ \frac{6}{21}$
The denominators are different (63 and 21).
Find the LCM of the denominators: LCM(63, 21) = 63 (since $21 \times 3 \ = \ 63$).
Convert $\frac{6}{21}$ to an equivalent fraction with denominator 63:
$\frac{6}{21} \ = \ \frac{6 \times 3}{21 \times 3} \ = \ \frac{18}{63}$
Now add the fractions:
$\frac{5}{63} \ + \ \frac{18}{63} \ = \ \frac{5 \ + \ 18}{63} \ = \ \frac{23}{63}$
Therefore, the result is $\frac{23}{63}$.
(iii) $\frac{-6}{13} \ - \ \left( \frac{-7}{15} \right)$
Given expression: $\frac{-6}{13} \ - \ \left( \frac{-7}{15} \right)$
Solution:
Subtracting a negative number is the same as adding the positive counterpart:
$\frac{-6}{13} \ - \ \left( \frac{-7}{15} \right) \ = \ \frac{-6}{13} \ + \ \frac{7}{15}$
The denominators are different (13 and 15).
Find the LCM of the denominators: LCM(13, 15) = $13 \times 15 \ = \ 195$. (Since 13 and 15 are co-prime).
Convert the fractions to equivalent fractions with denominator 195:
$\frac{-6}{13} \ = \ \frac{-6 \times 15}{13 \times 15} \ = \ \frac{-90}{195}$
$\frac{7}{15} \ = \ \frac{7 \times 13}{15 \times 13} \ = \ \frac{91}{195}$
Now add the equivalent fractions:
$\frac{-90}{195} \ + \ \frac{91}{195} \ = \ \frac{-90 \ + \ 91}{195} \ = \ \frac{1}{195}$
Therefore, the result is $\frac{1}{195}$.
(iv) $\frac{-3}{8} \ - \ \frac{7}{11}$
Given expression: $\frac{-3}{8} \ - \ \frac{7}{11}$
Solution:
The denominators are different (8 and 11).
Find the LCM of the denominators: LCM(8, 11) = $8 \times 11 \ = \ 88$. (Since 8 and 11 are co-prime).
Convert the fractions to equivalent fractions with denominator 88:
$\frac{-3}{8} \ = \ \frac{-3 \times 11}{8 \times 11} \ = \ \frac{-33}{88}$
$\frac{7}{11} \ = \ \frac{7 \times 8}{11 \times 8} \ = \ \frac{56}{88}$
Now subtract the fractions:
$\frac{-33}{88} \ - \ \frac{56}{88} \ = \ \frac{-33 \ - \ 56}{88} \ = \ \frac{-89}{88}$
Therefore, the result is $\frac{-89}{88}$ or $-1\frac{1}{88}$.
(v) $-2\frac{1}{9} \ - \ 6$
Given expression: $-2\frac{1}{9} \ - \ 6$
Solution:
First, convert the mixed fraction into an improper fraction:
$-2\frac{1}{9} \ = \ -\frac{(2 \times 9) \ + \ 1}{9} \ = \ -\frac{18 \ + \ 1}{9} \ = \ \frac{-19}{9}$
Write 6 as a fraction with denominator 1: $6 \ = \ \frac{6}{1}$.
Now the expression is $\frac{-19}{9} \ - \ \frac{6}{1}$.
The denominators are different (9 and 1).
Find the LCM of the denominators: LCM(9, 1) = 9.
Convert $\frac{6}{1}$ to an equivalent fraction with denominator 9:
$\frac{6}{1} \ = \ \frac{6 \times 9}{1 \times 9} \ = \ \frac{54}{9}$
Now subtract the fractions:
$\frac{-19}{9} \ - \ \frac{54}{9} \ = \ \frac{-19 \ - \ 54}{9} \ = \ \frac{-73}{9}$
We can convert this back to a mixed fraction:
$\frac{-73}{9} \ = \ -8\frac{1}{9}$
Therefore, the result is $\frac{-73}{9}$ or $-8\frac{1}{9}$.
Question 3. Find the product:
(i) $\frac{9}{2} × \left( \frac{-7}{4} \right)$
(ii) $\frac{3}{10} × (-9)$
(iii) $\frac{-6}{5} × \frac{9}{11}$
(iv) $\frac{3}{7} × \left( \frac{-2}{5} \right)$
(v) $\frac{3}{11} × \frac{2}{5}$
(vi) $\frac{3}{-5} × \frac{-5}{3}$
Answer:
(i) $\frac{9}{2} \ \times \ \left( \frac{-7}{4} \right)$
Given expression: $\frac{9}{2} \ \times \ \frac{-7}{4}$
Solution:
Multiply the numerators and the denominators:
$\frac{9 \ \times \ (-7)}{2 \ \times \ 4} \ = \ \frac{-63}{8}$
The fraction $\frac{-63}{8}$ is already in its simplest form.
Therefore, the product is $\frac{-63}{8}$ or $-7\frac{7}{8}$.
(ii) $\frac{3}{10} \ \times \ (-9)$
Given expression: $\frac{3}{10} \ \times \ (-9)$
Solution:
Write $-9$ as a fraction: $-9 \ = \ \frac{-9}{1}$.
The expression becomes $\frac{3}{10} \ \times \ \frac{-9}{1}$.
Multiply the numerators and the denominators:
$\frac{3 \ \times \ (-9)}{10 \ \times \ 1} \ = \ \frac{-27}{10}$
The fraction $\frac{-27}{10}$ is already in its simplest form.
Therefore, the product is $\frac{-27}{10}$ or $-2\frac{7}{10}$.
(iii) $\frac{-6}{5} \ \times \ \frac{9}{11}$
Given expression: $\frac{-6}{5} \ \times \ \frac{9}{11}$
Solution:
Multiply the numerators and the denominators:
$\frac{-6 \ \times \ 9}{5 \ \times \ 11} \ = \ \frac{-54}{55}$
The fraction $\frac{-54}{55}$ is already in its simplest form.
Therefore, the product is $\frac{-54}{55}$.
(iv) $\frac{3}{7} \ \times \ \left( \frac{-2}{5} \right)$
Given expression: $\frac{3}{7} \ \times \ \frac{-2}{5}$
Solution:
Multiply the numerators and the denominators:
$\frac{3 \ \times \ (-2)}{7 \ \times \ 5} \ = \ \frac{-6}{35}$
The fraction $\frac{-6}{35}$ is already in its simplest form.
Therefore, the product is $\frac{-6}{35}$.
(v) $\frac{3}{11} \ \times \ \frac{2}{5}$
Given expression: $\frac{3}{11} \ \times \ \frac{2}{5}$
Solution:
Multiply the numerators and the denominators:
$\frac{3 \ \times \ 2}{11 \ \times \ 5} \ = \ \frac{6}{55}$
The fraction $\frac{6}{55}$ is already in its simplest form.
Therefore, the product is $\frac{6}{55}$.
(vi) $\frac{3}{-5} \ \times \ \frac{-5}{3}$
Given expression: $\frac{3}{-5} \ \times \ \frac{-5}{3}$
Solution:
First, write $\frac{3}{-5}$ in standard form: $\frac{-3}{5}$.
The expression becomes $\frac{-3}{5} \ \times \ \frac{-5}{3}$.
Multiply the numerators and the denominators:
$\frac{(-3) \ \times \ (-5)}{5 \ \times \ 3} \ = \ \frac{15}{15}$
Simplify the fraction:
$\frac{15}{15} \ = \ 1$
Alternatively, we can cancel common factors before multiplying:
$\frac{\cancel{3}^{\;1}}{\cancel{-5}_{\;-1}} \ \times \ \frac{\cancel{-5}^{\;-1}}{\cancel{3}_{\;1}} \ = \ \frac{1}{-1} \ \times \ \frac{-1}{1} \ = \ (-1) \ \times \ (-1) \ = \ 1$
Therefore, the product is 1.
Question 4. Find the value of:
(i) $(-4) ÷ \frac{2}{3}$
(ii) $\frac{-3}{5} ÷ 2$
(iii) $\frac{-4}{5} ÷ (-3)$
(iv) $\frac{-1}{8} ÷ \frac{3}{4}$
(v) $\frac{-2}{13} ÷ \frac{1}{7}$
(vi) $\frac{-7}{12} ÷ \left( \frac{-2}{13} \right)$
(vii) $\frac{3}{13} ÷ \left( \frac{-4}{65} \right)$
Answer:
(i) $(-4) \ \div \ \frac{2}{3}$
Given expression: $(-4) \ \div \ \frac{2}{3}$
Solution:
Write $-4$ as a fraction: $-4 \ = \ \frac{-4}{1}$.
Division by a rational number is equivalent to multiplication by its reciprocal.
The reciprocal of $\frac{2}{3}$ is $\frac{3}{2}$.
So, the expression becomes: $\frac{-4}{1} \ \times \ \frac{3}{2}$.
Multiply the numerators and the denominators:
$\frac{-4 \ \times \ 3}{1 \ \times \ 2} \ = \ \frac{-12}{2}$
Simplify the fraction:
$\frac{-12}{2} \ = \ -6$
Therefore, the value is -6.
(ii) $\frac{-3}{5} \ \div \ 2$
Given expression: $\frac{-3}{5} \ \div \ 2$
Solution:
Write $2$ as a fraction: $2 \ = \ \frac{2}{1}$.
The expression becomes: $\frac{-3}{5} \ \div \ \frac{2}{1}$.
Multiply by the reciprocal of $\frac{2}{1}$, which is $\frac{1}{2}$.
$\frac{-3}{5} \ \times \ \frac{1}{2}$
Multiply the numerators and the denominators:
$\frac{-3 \ \times \ 1}{5 \ \times \ 2} \ = \ \frac{-3}{10}$
Therefore, the value is $\frac{-3}{10}$.
(iii) $\frac{-4}{5} \ \div \ (-3)$
Given expression: $\frac{-4}{5} \ \div \ (-3)$
Solution:
Write $-3$ as a fraction: $-3 \ = \ \frac{-3}{1}$.
The expression becomes: $\frac{-4}{5} \ \div \ \frac{-3}{1}$.
Multiply by the reciprocal of $\frac{-3}{1}$, which is $\frac{1}{-3}$ or $\frac{-1}{3}$.
$\frac{-4}{5} \ \times \ \frac{-1}{3}$
Multiply the numerators and the denominators:
$\frac{(-4) \ \times \ (-1)}{5 \ \times \ 3} \ = \ \frac{4}{15}$
Therefore, the value is $\frac{4}{15}$.
(iv) $\frac{-1}{8} \ \div \ \frac{3}{4}$
Given expression: $\frac{-1}{8} \ \div \ \frac{3}{4}$
Solution:
Multiply by the reciprocal of $\frac{3}{4}$, which is $\frac{4}{3}$.
$\frac{-1}{8} \ \times \ \frac{4}{3}$
Multiply the numerators and the denominators:
$\frac{-1 \ \times \ 4}{8 \ \times \ 3} \ = \ \frac{-4}{24}$
Simplify the fraction by dividing the numerator and denominator by their GCD, which is 4:
$\frac{-4 \div 4}{24 \div 4} \ = \ \frac{-1}{6}$
Alternatively, cancel common factors before multiplying:
$\frac{-1}{\cancel{8}_{\;2}} \ \times \ \frac{\cancel{4}^{\;1}}{3} \ = \ \frac{-1 \ \times \ 1}{2 \ \times \ 3} \ = \ \frac{-1}{6}$
Therefore, the value is $\frac{-1}{6}$.
(v) $\frac{-2}{13} \ \div \ \frac{1}{7}$
Given expression: $\frac{-2}{13} \ \div \ \frac{1}{7}$
Solution:
Multiply by the reciprocal of $\frac{1}{7}$, which is $\frac{7}{1}$.
$\frac{-2}{13} \ \times \ \frac{7}{1}$
Multiply the numerators and the denominators:
$\frac{-2 \ \times \ 7}{13 \ \times \ 1} \ = \ \frac{-14}{13}$
Therefore, the value is $\frac{-14}{13}$ or $-1\frac{1}{13}$.
(vi) $\frac{-7}{12} \ \div \ \left( \frac{-2}{13} \right)$
Given expression: $\frac{-7}{12} \ \div \ \left( \frac{-2}{13} \right)$
Solution:
Multiply by the reciprocal of $\frac{-2}{13}$, which is $\frac{13}{-2}$ or $\frac{-13}{2}$.
$\frac{-7}{12} \ \times \ \frac{-13}{2}$
Multiply the numerators and the denominators:
$\frac{(-7) \ \times \ (-13)}{12 \ \times \ 2} \ = \ \frac{91}{24}$
Therefore, the value is $\frac{91}{24}$ or $3\frac{19}{24}$.
(vii) $\frac{3}{13} \ \div \ \left( \frac{-4}{65} \right)$
Given expression: $\frac{3}{13} \ \div \ \left( \frac{-4}{65} \right)$
Solution:
Multiply by the reciprocal of $\frac{-4}{65}$, which is $\frac{65}{-4}$ or $\frac{-65}{4}$.
$\frac{3}{13} \ \times \ \frac{-65}{4}$
Cancel common factors before multiplying (13 is a factor of 65, $65 \ = \ 13 \ \times \ 5$):
$\frac{3}{\cancel{13}_{\;1}} \ \times \ \frac{-\cancel{65}^{\;5}}{4} \ = \ \frac{3 \ \times \ (-5)}{1 \ \times \ 4} \ = \ \frac{-15}{4}$
Alternatively, multiply first:
$\frac{3 \ \times \ (-65)}{13 \ \times \ 4} \ = \ \frac{-195}{52}$
Simplify by dividing by the GCD(195, 52). $195 \ = \ 3 \ \times \ 5 \ \times \ 13$, $52 \ = \ 4 \ \times \ 13$. GCD is 13.
$\frac{-195 \div 13}{52 \div 13} \ = \ \frac{-15}{4}$
Therefore, the value is $\frac{-15}{4}$ or $-3\frac{3}{4}$.

